Simplex and Complex Sound
- Olive Ghosh

- Jun 16, 2023
- 3 min read
Sine waves have a very pure sound because they consist of energy at only one frequency and are often called pure tones. They are not heard very commonly in real life (although they can be generated electrically) since most sound sources do not vibrate in such a simple manner. A person whistling or a recorder (a simple wind instrument) produces a sound which approaches a sinusoidal waveform. Most real sounds are made up of a combination of vibration patterns which result in a more complex waveform. The more complex the waveform, the more like noise the sound becomes, and when the waveform has a highly random pattern the sound is said to be noise.
The important characteristic of sounds which have a definite pitch is that they are repetitive: that is, the waveform, no matter how complex, repeats its pattern in the same way at regular intervals. All such waveforms can be broken down into a series of components known as harmonics, using a mathematical process called Fourier analysis.
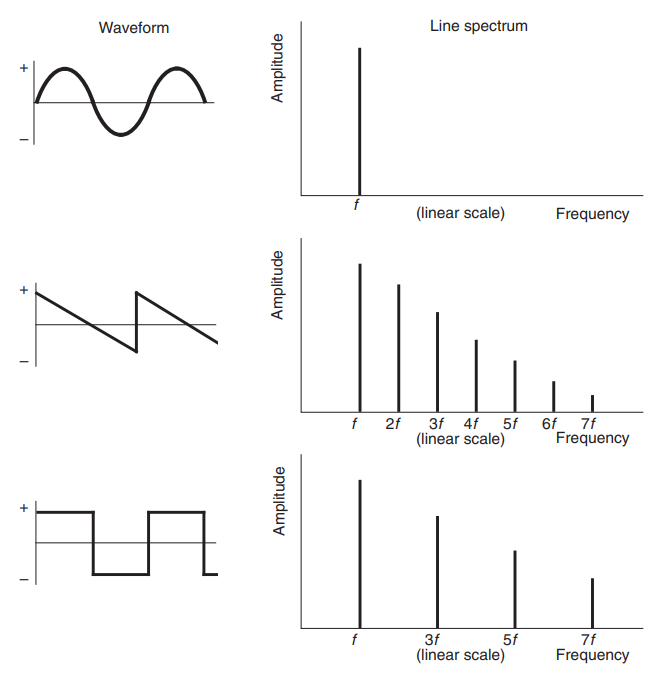
This figure shows another way of depicting the characteristics of the sound graphically –that is, by drawing a so-called line spectrum which shows frequency along the horizontal axis and amplitude up the vertical axis. The line spectrum shows the relative strengths of different frequency components which make up a sound. Where there is a line there is a frequency component. It will be noticed that the more complex the waveform the more complex the corresponding line spectrum.
For every waveform, there is a corresponding line spectrum: waveforms and line spectra are simply two different ways of showing the characteristics of the sound. Figure 1.3 is called a time-domain plot, whilst the line spectrum is called a frequency-domain plot. Unless otherwise stated, such frequency-domain graphs in this book will cover the audio-frequency range, from 20 Hz at the lower end to 20kHz at the upper end.
In a reversal of the above breaking-down of waveforms into their component frequencies it is also possible to construct or synthesize waveforms by adding together the relevant components.
The simple sine wave has a line spectrum consisting of only one component at the frequency of the sine wave. This is known as the fundamental frequency of oscillation. The other repetitive waveforms, such as the square wave, have a fundamental frequency as well as a number of additional components above the fundamental. These are known as harmonics but may also be referred to as overtones or partials.
Harmonics are frequency components of a sound which occur at integer multiples of the fundamental frequency, that is at twice, three times, four times and so on. Thus, a sound with a fundamental of 100 Hz might also contain harmonics at 200 Hz, 400 Hz and 600 Hz.
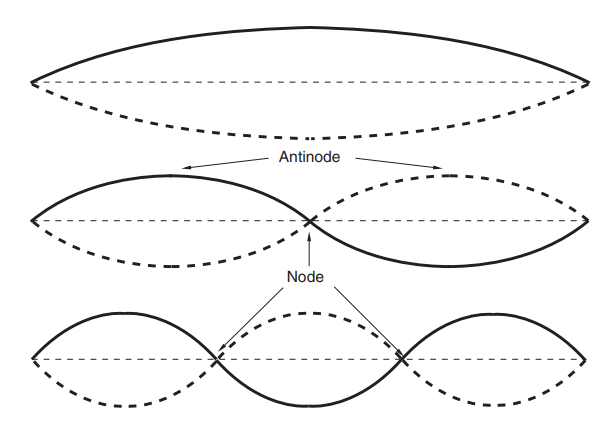
Consider a stretched string, as shown in Figure. It may be made to vibrate in any of a number of modes, corresponding to integer multiples of the fundamental frequency of vibration of the string (the concept of ‘standing waves’ is introduced below). The fundamental corresponds to the mode in which the string moves up and down as a whole, whereas the harmonics correspond to modes in which the vibration pattern is divided into points of maximum and minimum motion along the string (these are called antinodes and nodes). It will be seen that the second mode involves two peaks of vibration, the third mode three peaks, and so on.
In accepted terminology, the fundamental is also the first harmonic, and thus the next component is the second harmonic, and so on. Confusingly, the second harmonic is also known as the first overtone. For the waveforms shown in Figure, the fundamental has the highest amplitude, and the amplitudes of the harmonics decrease with increasing frequency, but this will not always be the case with real sounds since many waveforms have line spectra which show the harmonics to be higher in amplitude than the fundamental. It is also quite feasible for there to be harmonics missing in the line spectrum, and this depends entirely on the waveform in question.
It is also possible for there to be overtones in the frequency spectrum of a sound which are not related in a simple integer-multiple fashion to the fundamental. These cannot correctly be termed harmonics, and they are more correctly referred to as overtones or inharmonic partials. They tend to arise in vibrating sources which have a complicated shape, and which do not vibrate in simple harmonic motion but have a number of repetitive modes of vibration. Their patterns of oscillation are often unusual, such as might be observed in a bell or a percussion instrument. It is still possible for such sounds to have a recognizable pitch, but this depends on the strength of the fundamental. In bells and other such sources, one often hears the presence of several strong inharmonic overtones.
Bibliography:
Sound and Recording, Sixth Edition, Francis Rumsey and Tim McCormick.
Designing Sound, MIT
Sound Design, Maurizio Giri.





Comments